LAS ECUACIONES MATEMÁTICAS QUE SON CONSIDERADAS LAS MÁS HERMOSAS.
Las ecuaciones matemáticas representan algunas de las leyes más complejas que gobiernan el Universo y todo lo que hay en ello.
Se necesita años de experiencia para entender las ecuaciones más profundas y muchas de ellas son tan complejas que son difíciles de traducir a un lenguaje normal.
Sin embargo, esto no significa que no podamos apreciar su belleza.
A continuación conoceremos esas ecuaciones que son consideradas las mas hermosas por su aporte al mundo.
La ecuación de Dirac
"Estéticamente es elegante y simple"
"Es una ecuación muy poderosa por lo que significa y su papel en la historia de la física del siglo XX".
La ecuación fue descubierta a finales de los años 20 por el físico Paul Dirac, y juntó dos de las ideas más importantes de la ciencia: la mecánica cuántica, que describe el comportamiento de objetos muy pequeños; y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido.
Por lo tanto, la ecuación de Dirac describe cómo las partículas como electrones se comportan cuando viajan a casi la velocidad de la luz.
La fórmula de Riemann
El matemático Bernhard Riemann publicó esta ecuación en 1859.
Permite calcular los números primos por debajo de un número dado.
Por ejemplo, la ecuación de Riemann revela que hay 24 números primos entre 1 y 100.
"Los números primos son los átomos de la aritmética", explica Marcus du Sautoy de la universidad de Oxford.
"Son los números más básicos e importantes en el corazón del mundo de la matemática. Pero sorprendentemente, a pesar de más de 2000 años de investigación, todavía no los entendemos".
Pi
Muchos lectores sabrán de esta famosa ecuación.
Sencillamente describe cómo la circunferencia de un círculo varía con su diámetro.
La relación de los dos es un número llamado pi, que aproximadamente es 3,14, pero no exactamente.
Pi es un número irracional, lo que significa que los dígitos pueden continuar indefinidamente sin que se repitan.
Euler-Lagrange
Esta ecuación se utiliza para analizar todo, desde la forma de una burbuja de jabón a la trayectoria de un cohete alrededor de un agujero negro.
"Más que una ecuación, es una receta para generar una infinita variedad de posibles leyes de física", comenta Andrew Pontzen de la University College London.
A pesar de sus múltiples aplicaciones, la ecuación es "engañosamente corta y simple",
La ecuación de Yang-Baxter
"La ecuación de Yang-Baxter es una ecuación simple que puede ser representada en un dibujo de un niño de dos años".
Como la ecuación de Euler-Lagrange, se ve simple pero tiene implicaciones profundas en muchas áreas de la matemática y la física.
Esto incluye cómo se comportan las olas en aguas poco profundas, la interacción de partículas subatómicas, la teoría matemática de nudos y la teoría de las cuerdas.
"Te lo puedes imaginar como estar en el centro de una telaraña", explica Weston. "En las cuerdas de esa red puedes encontrar muchos temas en lo que juega un papel fundamental".
Identidad de Euler
"La mayoría de las matemáticas modernas y físicas derivan del trabajo de Leonhard Euler"
Él fue "el matemático más prolífico de todos los tiempos" y el "Mozart de las matemáticas".
Pero a pesar de todos sus logros, "mucha de la autocalificada 'gente educada' nunca ha oído hablar de él".
Su ecuación más famosa es la identidad de Euler, y en ella se pueden vincular las constantes de la matemática.
La ecuación combina cinco de los números más importantes de la matemática. Los cuales son:
1 – la base de todos los números
0 – el concepto de la nada
pi – el número que define al círculo
e – el número que subraya el crecimiento exponencial
i – la raíz cuadrada "imaginaria" de -1
Todos los números tienen aplicaciones prácticas, incluida para la comunicación, navegación, energía, fabricación, finanzas, meteorología y medicina.
Pero eso no es todo: la identidad de Euler también tiene tres de las operaciones matemáticas más básicas: suma, resta y exponenciación.Gracias por llegar hasta el final, hasta la próxima!!!🙋🙋🙋
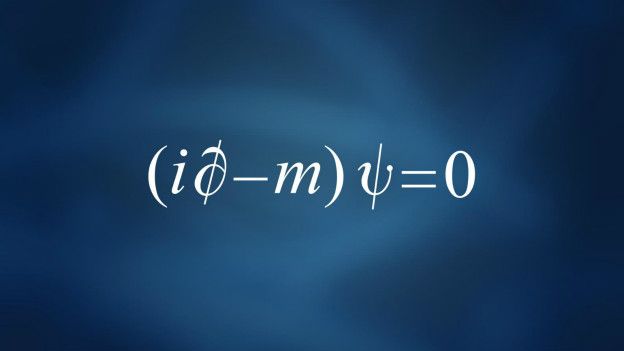


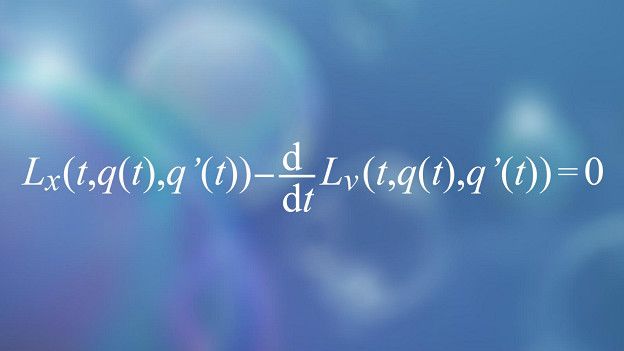

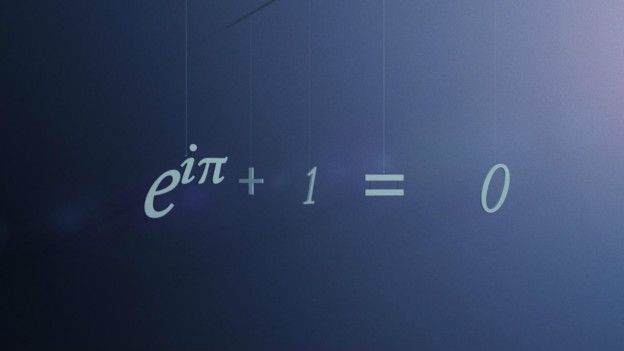

Excelente información...
ResponderEliminarQue bonita información
ResponderEliminarQue interesante contenido
ResponderEliminarGracias por compartir la información, esta muy bonita
ResponderEliminarexcelente
ResponderEliminar